1. The Pattern Idea

The central idea of creation is simple; there is a Pattern behind it all.

Examples of patterns and their manifestations

Light: One sun can radiate many colours.

Music: One flute can make many music notes.

Words: One mouth can speak many words.

Information: One code can make many messages.

Pottery: One mould can make many pots.

The Pattern could be compared, by analogy, to a single object that produces light, music, speech and messages, but also tangible things.

2. The Pattern Theorem

A linear inverse symmetric pair of quantities yield a conserved sum.

a>+<b = [c]

The pair of quantities is a and b and their sum is c. The Pattern values for a and b are positive integers:

a = 6,5,4,3,2,1,0 and b = 0,1,2,3,4,5,6.

The two arrow symbols reflect the deceasing values of a and the increasing values of b.

The equation is represented by a geometric module.

(a + b) could be raised to any power, e.g. (a + b)³

3. The Pattern Law

The Pattern sum is conserved.
‘Conserved’ means that the sum is invariant or constant.

[c]

The Pattern law is similar to the First Law of Thermodynamics, the energy conservation law.

(Work increases while heat decreases and vice versa.)

The Pattern law is more general than the energy law because its definition does not involve any physical quantity, such as heat.

The Pattern law implies that anything develops, e.g. manifest, grow and move, from something pre-existing.

4. The Pattern vs Pythagoras

The Pattern is better than Pythagoras

because

the Pythagoras sum cannot be cubed*

(Pythagoras: a² + b² = c²)

but

the Pattern sum can be cubed.

(The Pattern: (a + b)³ = c³)

The Pythagoras geometry is based on squares, the Pattern geometry on squares and cubes.

The Pythagoras equation, with the Pattern values, yield nonlinear structures whereas the Pattern equations always yield linear structures.

*According to Fermat’s Last Theorem.

5. The Pattern Cube

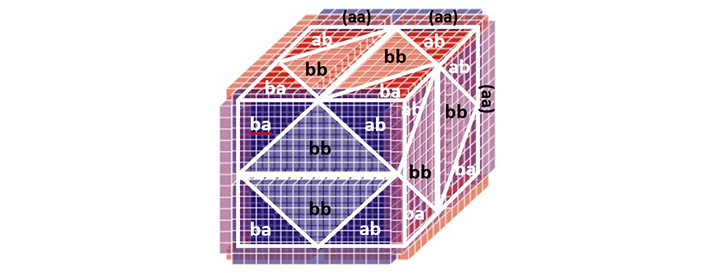
The Pattern cube is the geometric equivalent of the cubed Pattern sum pair. The Pattern cube is, therefore, a conserved object (a kind of mould) that represents the Pattern law.

The cubed sum pair [c³ & c³] is equivalent to 6 x [c² & c²]. This explains the squared terms, e.g. bb, of the cube.)

The Pattern cube is the generic cube. Specific cubes are defined by their individual pairs of quantities a,b.

6. The Atom Cube

The Atom cube contains all types of elementary particles, such as leptons and quarks.

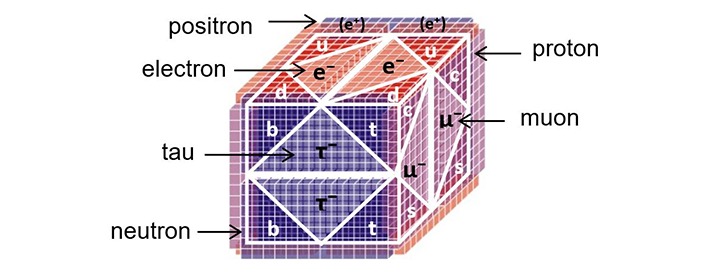
The Standard cube is a field version of the Standard Model and the Atom cube is a particle version.

The Standard cube also represents the periodic tables of electron, muon and tau atoms.

The Atom cube is a specific cube, an instance, of the Pattern cube.

7. The Gravity Cube

The Gravity cube represents three types of gravity.

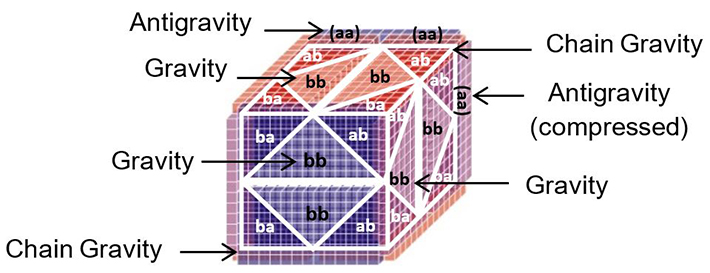
Gravity equals constant acceleration, i.e. 1², 2², 3². .

Chain gravity is acceleration and deceleration combined.

The Gravity cube is a specific cube, an instance, of the Pattern cube.

8. One Pattern, One Cosmos

Different instances of the Pattern cube, such as the Atom cube and Gravity cube, match different types of natural phenomena.

The cube matches confirm that fundamental things develop, e.g. manifest, grow and move, according to the law of the Pattern.

The ‘Ideas’ of Plato agree with the Pattern idea. Plato’s ideas (forms) exist in a separate (higher) dimension. Material things are simply their shadows.

The origin of the Pattern lies outside of the realm of science but Douglas Hofstadter wrote:

‘Where there’s pattern, there’s reason.’